Mohr 2015 Metrologia
| Mohr Peter J, Phillips William D (2015) Dimensionless units in the SI. Metrologia 52:40-7. https://doi.org/10.1088/0026-1394/52/1/40 |
Mohr Peter J, Phillips William D (2015) Metrologia
Abstract: The International System of Units (SI) is supposed to be coherent. That is, when a combination of units is replaced by an equivalent unit, there is no additional numerical factor. Here we consider dimensionless units as defined in the SI, e.g. angular units like radians or steradians and counting units like radioactive decays or molecules. We show that an incoherence may arise when different units of this type are replaced by a single dimensionless unit, the unit 'one', and suggest how to properly include such units into the SI in order to remove the incoherence. In particular, we argue that the radian is the appropriate coherent unit for angles and that hertz is not a coherent unit in the SI. We also discuss how including angular and counting units affects the fundamental constants.
• Bioblast editor: Gnaiger E
Discussion
- Count
- Gnaiger 2020 MitoFit x
- Lipp Melanie (2016) Molar standards & information units in the ’new-SI’. hal-01381003 - https://hal.archives-ouvertes.fr/hal-01381003
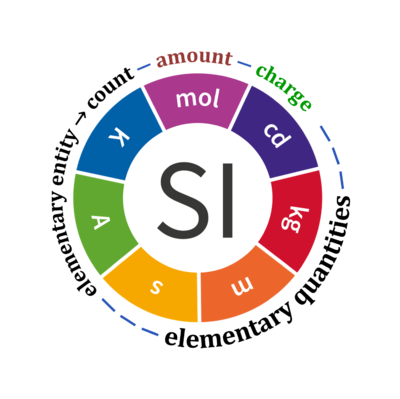
Quantity Symbol for quantity Q Symbol for dimension Name of abstract unit uQ Symbol for unit uQ [*] elementary entity *,$ UX U elementary unit x count *,$ NX = N·UX X elementary unit x amount of substance *,§ nX = NX·NA-1 N mole mol charge *,€ Qel = zX·e·NX I·T coulomb C = A·s length l L meter m mass m M kilogram kg time t T second s electric current I I ampere A thermodynamic temperature T Θ kelvin K luminous intensity Iv J candela cd
- [*] SI units, except for the canonical 'elementary unit' [x]. The following footnotes are canonical comments, related to iconic symbols.
- * For the elementary quantities NX, nX, and Qel, the entity-type X of the elementary entity UX has to be specified in the text and indicated by a subscript: nO2; Nce; Qel.
- $ Count NX equals the number of elementary entities UX. In the SI, the quantity 'count' is explicitly considered as an exception: "Each of the seven base quantities used in the SI is regarded as having its own dimension. .. All other quantities, with the exception of counts, are derived quantities" (Bureau International des Poids et Mesures 2019 The International System of Units (SI)). An elementary entity UX is a material unit, it is not a count (UX is not a number of UX). NX has the dimension X of a count and UX has the dimension U of an elementary entity; both quantities have the same abstract unit, the 'elementary unit' [x].
- § Amount nX is an elementary quantity, converting the elementary unit [x] into the SI base unit mole [mol] using the Avogadro constant NA.
- € Charge is a derived SI quantity. Charge is an elementary quantity, converting the elementary unit [x] into coulombs [C] using the elementary charge e, or converting moles [mol] into coulombs [C] using the Faraday constant F. zX is the charge number per elementary entity UX, which is a constant for any defined elementary entity UX. Qel = zX·F·nX
Cited by
- Gnaiger E (2020) Mitochondrial pathways and respiratory control. An introduction to OXPHOS analysis. 5th ed. Bioenerg Commun 2020.2. https://doi.org/10.26124/bec:2020-0002
- Gnaiger E et al ― MitoEAGLE Task Group (2020) Mitochondrial physiology. Bioenerg Commun 2020.1. doi:10.26124/bec:2020-0001.v1.
Labels:
Count, Avogadro constant, BEC 2020.1, BEC 2020.2